С. Ф. Добкин
Наборное оформление различных видов текста
Математические формулы

Математические формулы

Язык формул — особый и, добавим, международный язык. У него свои, твердо установленные правила. Каждый элемент формулы — буква, цифра, знак— обозначает определенное понятие. К тому же каждый из этих элементов может получить иное значение, если изменить характер его начертания, размер и расположение. Поэтому для того, чтобы смысл формул не искажался и был ясен читателям, в их наборном оформлении необходима логичная, общепризнанная и последовательно проводимая система. Эта система определяет в основном характер (начертание) применяемых шрифтов и специальных знаков, их кегль, а также взаимное расположение частей и элементов формулы.

Формулу, набранную бессистемно, труднее прочитать и понять, однако только опытный глаз может сразу определить, в чем ее наборное оформление неправильно или непоследовательно, что в нем надо упорядочить. Поэтому в приводимых далее примерах показаны некоторые сложные случаи наборного оформления формул. Внимательное рассмотрение их поможет читателю яснее понять основные положения системы, о которой мы упоминали.

Цифры в формулах служат для обозначения чисел, как и в любом другом тексте; поэтому для них применяется шрифт обычного, т. е. прямого светлого начертания.

Для условных обозначений величин (символов) используют буквы латинского, а также греческого и (реже) готического алфавитов.

Буквы латинского алфавита, обозначающие величины, применяются в курсивном начертании; так они резче отличаются и не могут быть спутаны при чтении с элементами обычного текста (например, обозначение величины а отличается от союза «а», величины с — от предлога «с»). В некоторых разделах математики необходимы буквы латинского алфавита двух начертаний. В качестве второго принято прямое полужирное, причем обычно не своей гарнитуры, а какой-либо гротесковой (для более сильного выделения).

Буквы греческого и готического алфавитов могут применяться как прямого, так и курсивного начертания (в обоих начертаниях они достаточно отличаются от русских и латинских), но единообразно во всем издании.

Для условных сокращений математических терминов (например, sin, arctg, lim, max) тоже применяется шрифт латинского алфавита, но в прямом начертании (в отличие от обозначений величин). По аналогии прямой шрифт используют и в тех случаях, когда условные сокращения даны буквами русского алфавита (например, c_н в смысле c нормальное, в отличие от с_n, то есть с энное).

Сокращенные наименования метрических мер и технических единиц измерения, обозначенные буквами латинского алфавита, тоже даются прямым шрифтом (50 kg, 120 v). Если же они обозначаются буквами русского алфавита, то обычно,— но не обязательно, применяется курсив (50 кг, 120 в).

Что касается кегля, то для однострочных формул (за исключением индексов, показателей степени и некоторых специальных знаков) обычно используют шрифт того же кегля, что и для основного текста книги.

Двухстрочные же (или многострочные) части формулы, то есть дроби, набираются двояко — шрифтом такого же кегля, что и однострочные формулы, или же шрифтом несколько пониженного кегля, например петитом, если однострочные части формул набираются корпусом (пример 20).

Каждый из этих способов имеет свои достоинства и недостатки. В первом случае одна и та же величина в любой формуле данного издания изображается буквой или цифрой одинакового кегля, что вполне логично. Однако при этом формула менее компактна. Во втором — строгая логичность в какой-то мере нарушается, но зато формула становится компактнее, и хорошо подготовленный читатель легче охватит ее глазом. Кроме того, этот способ экономичнее первого.

В практике советских издательств первый способ применяется в книгах для малоподготовленного читателя, в частности в учебниках для средней школы, где к тому же формулы несложны и легко охватываются глазом, если даже двухстрочия набраны корпусом. В книгах для подготовленного читателя (в научной литературе) до недавнего времени пользовались вторым способом. Однако в последние годы произошли изменения в технике набора — стало возможным набирать двухстрочные и даже четырехстрочные формулы на наборных и фотонаборных машинах, но обычно при одинаковом кегле для однострочных и двухстрочных (многострочных) частей формулы.

Показатели степени и индексы должны быть значительно меньше букв и цифр в основной строке, чтобы четко отличаться от них, и примерно наполовину выступать над (или под) выражением, к которому они относятся.

Математические знаки четырех действий, знаки геометрических образов, а также знаки, показывающие соотношение левой и правой частей формулы, набираются таким же кеглем, как и вся строка, к которой они относятся.

Однако для некоторых знаков необходим больший размер:

• скобки должны охватывать (по высоте) все заключенное в них выражение;
• знак радикала v должен соответствовать по высоте подкоренному выражению вместе с приставной линейкой, прикрывающей это выражение сверху;
• знаки суммы ?, произведения ? и интеграла ? относятся к целому выражению; сигналом этого является их более крупный кегль по сравнению с другими элементами формулы: в однострочных — на 2–4 пункта, а в двухстрочных и многострочных — сообразно высоте формулы (пример 21).

Отдельные части формулы необходимо отбить (отделить) одну от другой. Нормальная величина каждого пробела внутри формулы — 2 пункта (при наборе нонпарелью — 1 пункт).

Отбивку внутри формул производят в следующих случаях:

знаки, выражающие соотношение между левой и правой частями формулы (=, ?, >,<), знаки действий (+,?,?,•,:), знаки геометрических образов (L,?), а также сокращенные обозначения тригонометрических функций и других математических терминов отделяют пробелом как от предыдущей, так и от последующей частей формулы; знак извлечения корня (радикал) отбивают только от предшествующей части формулы, не отделяя его от подкоренного выражения. Знак препинания, помещенный после формулы, не отделяется от нее.

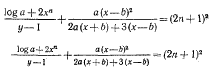
Пример 20
Наборное оформление формулы, часть которой
однострочная, а часть — двухстрочная

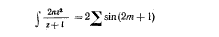
Пример 21
Наборное оформление формулы со знаками
суммы и интеграла

Цифры и буквенные обозначения величин, следующие одни за другими и не разделенные какими-либо знаками, не отделяются друг от друга; индексы и показатели степени тоже не отбиваются от тех элементов формулы, к которым они относятся.

В двухстрочном выражении (дроби) делительная линейка должна быть равна более длинной части дроби (числителю или знаменателю); более короткая часть дроби выключается на середину по отношению к формату этой линейки.

Делительная линейка в дроби должна приходиться против средней линии формулы, то есть против середины знаков =, + и т. п. в однострочной части формулы.

Трехстрочное выражение — это дробь, у которой либо числитель, либо знаменатель тоже дробный. Чтобы читатель мог сразу отличить основную дробь от вспомогательной (то есть от той, которая служит числителем или знаменателем основной дроби), делительная линейка основной дроби выделяется либо увеличенной длиной (на 4—8 пунктов длиннее линейки вспомогательной дроби), либо повышенной жирностью. Аналогичный способ применяется и для четырехстрочных выражений.

Формулы, расположенные отдельными строками, обычно выключают в красную строку, то есть на середину формата (при асимметричном расположении некоторых других элементов, например заголовков, и формулы могут быть выключены таким же образом).

Формула, которая расположена в подбор с текстом, обязательно отделяется достаточно заметным пробелом (не менее половины кегля шрифта) от предшествующего и следующего за ней текста.

Переносы в формулах нежелательны. Чтобы уместить формулу в формат строки и таким образом избежать переноса, можно уменьшить пробелы между элементами.

Если таким путем не удается довести длинную формулу до формата строки, то перенос делается в первую очередь на знаках соотношения между левой и правой ее частями (=, =, >, <); во вторую — на знаках сложения или вычитания (+, -), делящих формулу на члены; в третью — на знаке умножения (х), который для этой цели вводится в математическое выражение. При переносе нельзя разделять особенно тесно связанные между собой элементы формулы — дроби, выражения в скобках, а также выражения, относящиеся к знакам радикала, интеграла, суммы и произведения.

Если в дроби числитель или знаменатель не умещается в одну строку, можно применить один из следующих способов:

• набрать дробь шрифтом пониженного кегля;
• набрать числитель в две строки с переносом, поместив обе строки над линейкой (или знаменатель в две строки с переносом, поместив их под линейкой) (пример 22);
• преобразовать дробь, представив ее в виде суммы или произведения двух дробей, вторую из которых переносят в следующую строку; такое преобразование сравнительно несложно, но сделать его имеет право только автор или редактор.

Первый способ применим, если длина дроби лишь не намного превышает формат строки. Второй — особенно уместен, если переносимая часть дроби (числитель или знаменатель) не громоздка и в ней нет знаков радикала, интеграла и т. п. Третий — хорош при условии, что новая форма дроби будет вполне понятна читателю.

Вопрос о том, какой из перечисленных способов выбрать, должен быть согласован с редактором.

Во всех случаях переноса его знак повторяют два раза — в конце первой строки и в начале второй. Таким образом связь между обеими строками делается особенно заметной; благодаря этому читателю становится легче сразу охватить формулу глазом.

Переносимая формула может быть расположена двумя способами: по первому способу обе части (обе строки) формулы выключаются в красную строку; по второму же способу начало (первая строка формулы) выключается к левому краю формата или с небольшим отступом от него, а переносимая часть (вторая строка формулы) — к правому краю или с таким же отступом от него (пример 23).

При втором способе связь между обеими частями формулы более заметна.

Описанная система наборного оформления математических формул облегчает их восприятие, но некоторые положения ее приводят к тому, что формулы занимают довольно много места. Так, если формула (или какая-нибудь часть ее) представляет собой дробь, у которой знаменатель расположен под числителем и отделен от него горизонтальной чертой, то она (формула) занимает по высоте не одну строку, а немного больше двух; такую формулу нельзя набирать в подбор, а приходится помещать вразрез полосы и отбивать от предшествующего и последующего текста. В результате формула-дробь займет примерно четыре строки.

Разработаны некоторые изменения системы, позволяющие более экономно использовать площадь бумаги. Важнейшее из них заключается в том, что в дробях знаменатель располагается не под числителем, а в одной строке с ним и отделяется от него косой чертой.

При этом двухстрочная формула превращается в однострочную; знаки ?, ? и ? в однострочных формулах набирают шрифтом того же кегля, что и основную строку.

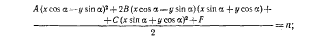
Пример 22
Наборное оформление трехстрочной математической формулы

Пример 23
Наборное оформление формулы c переносом

В таком виде формула не только занимает одну строку вместо двух, но и может быть помещена в подбор с текстом, а не выделена в отдельную строку.

Подобные приемы дают экономию бумаги, но затрудняют восприятие формул недостаточно подготовленным читателем. Поэтому они могут быть использованы в монографиях и статьях для специалистов, но их не применяют в учебниках.

 
‹‹ Назад  |  Оформление книги. Редактору и автору  |  Вперед ››